Cycles
From G-designs
Relevant articles: [1], [2], [3], [4], [5].
Contents[hide] |
Cycles
The graphs considered in this section are cycles. The cycle with 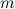 vertices is denoted by
vertices is denoted by  .
.
Spectrum Results
The spectrum problem for 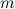 -cycles is completely solved for all
-cycles is completely solved for all 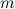 , see [2] and [4].
, see [2] and [4].
Notes
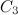 -designs are
-designs are 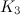 -designs.
-designs.
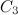 -designs are Steiner triple systems.
-designs are Steiner triple systems.
References
- ↑ Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ 2.0 2.1 2.2 Alspach, B. and Gavlas, H. Cycle decompositions of K_n and K_n-I, J. Combin. Theory Ser. B, 81, 77–99 (2001).
- ↑ Hoffman, D. G., Lindner, C. C., and Rodger, C. A. On the construction of odd cycle systems, J. Graph Theory, 13, 417–426 (1989).
- ↑ 4.0 4.1 4.2 Šajna, M. Cycle decompositions. III. Complete graphs and fixed length cycles, J. Combin. Des. 10, 27–78 (2002).
- ↑ Sotteau, D. Decomposition of K_m,n (K^^\ast _m,n) into cycles (circuits) of length 2k, J. Combin. Theory Ser. B, 30, 75–81 (1981).
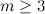 . There exists a
. There exists a 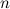 if and only if
if and only if
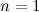 or
or 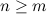 ;
;
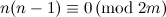 .
.