Wilson's Theorem
From G-designs
Wilson's Theorem
Theorem [1]
For any given graph 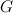 , there exists an integer
, there exists an integer  (
( is exponentially large) such that if
is exponentially large) such that if
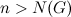 ;
;
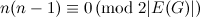 ; and
; and
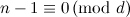 where
where 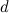 is the greatest common divisor of the degrees of the vertices in
is the greatest common divisor of the degrees of the vertices in 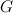 ,
,
then there exists a 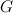 -design of order
-design of order 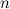 .
.
- ↑ Wilson, R. M. Decompositions of complete graphs into subgraphs isomorphic to a given graph, Proceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, No. XV, Utilitas Math., Winnipeg, Man. 647–659 (1976).