Matchings
From G-designs
Relevant articles: [1], [2], [3], [4].
Matchings
The graphs considered in this section are 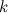 -matchings. A
-matchings. A 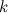 -matching is a graph consisting of
-matching is a graph consisting of 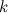 vertex disjoint edges and is denoted by
vertex disjoint edges and is denoted by 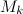 . The spectrum problem has been completely settled for matchings, see Theorem 1 below.
. The spectrum problem has been completely settled for matchings, see Theorem 1 below.
Spectrum Results
Theorem 1 is a consequence of results in [1], [2], [3] or [4].
Theorem 1
Let 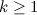 . There exists an
. There exists an 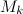 -design of order
-design of order 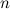 if and only if
if and only if
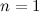 or
or 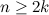 ; and
; and
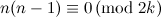 .
.
References
- ↑ 1.0 1.1 Alon, N. A note on the decomposition of graphs into isomorphic matchings, Acta Math. Hungar. 42, 221–223 (1983).
- ↑ 2.0 2.1 de Werra, D. On some combinatorial problems arising in scheduling, CORS J. 8, 165–175 (1970).
- ↑ 3.0 3.1 Ellingham, M. N. and Wormald, N. C. Isomorphic factorization of regular graphs and 3-regular multigraphs, J. London Math. Soc. (2), 37, 14–24 (1988).
- ↑ 4.0 4.1 McDiarmid, C. J. H. The solution of a timetabling problem, J. Inst. Math. Appl. 9, 23–34 (1972).