Miscellaneous

There are a few other graphs and families of graphs for which the spectrum problem has been considered but which are not covered in other sections. This page summarises the known results for the spectrum problem for the Petersen graph, the Heawood graph, dragons and 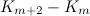$K_{m+2}-K_m$ .

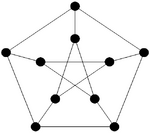
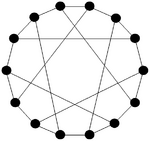
The Petersen graph and the Heawood graph are shown in Figure 1.

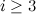*Figure 1: The Petersen graph and the Heawood graph.*
Petersen graph	Heawood graph

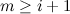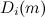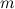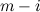For $i\geq 3$ and $m\geq i+1$ , let $D_i(m)$ denote the graph on $m$ vertices consisting of an $i$ -cycle and a path of $m-i$ edges which intersect in exactly one end-vertex of the path. These graphs are called dragons.

The spectrum problem for the graph obtained from a complete graph on 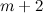$m+2$ vertices by removing the edges of a complete subgraph on 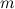$m$ vertices, denoted by 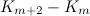$K_{m+2}-K_m$ has also been considered.

Spectrum Results

Theorem 1 _^[2]

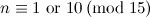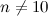Let $P$ denote the Petersen graph. There exists a $P$ -design of order $n$ if and only if $n \equiv 1 {\rm \ or \ } 10\,({\rm mod \ }15)$ and $n \neq 10$ .

Theorem 2 _^[3]

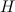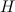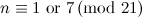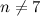Let $H$ denote the Heawood graph. There exists an $H$ -design of order $n$ if and only if $n \equiv 1 {\rm \ or \ } 7 \,({\rm mod \ }21)$ and $n\neq 7$ .

Theorem 3 _^[6]

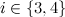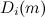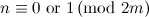For each $i \in \{3,4\}$ , a $D_i(m)$ -design of order $n$ exists if $n \equiv 0 {\rm \ or \ } 1\,({\rm mod \ }2m)$ . Moreover, this condition is also necessary when 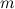$m$ is a power of $2$ .

Theorem 4 _^[1]

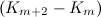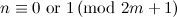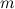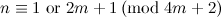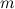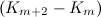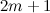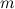There exists a $(K_{m+2}-K_m)$ -design of order $n$ for all $n \equiv 0 {\rm \ or \ } 1 \,({\rm mod \ }2m+1)$ when $m$ is even, and for all $n \equiv 1 {\rm \ or \ } 2m+1 \,({\rm mod \ }4m+2)$ when $m$ is odd, except that there is no $(K_{m+2}-K_m)$ -design of order $2m+1$ when $m$ is even.

References

↑ ^1.0 ^1.1 Adams, P., Billington, E. J., and Hoffman, D. G. On the spectrum for K_m+2\sbs K_m designs, J. Combin. Des. 5, 49–60 (1997).
↑ ^2.0 ^2.1 Adams, P. and Bryant, D. E. The spectrum problem for the Petersen graph, J. Graph Theory, 22, 175–180 (1996).
↑ ^3.0 ^3.1 Adams, P. and Bryant, D. E. The spectrum problem for the Heawood graph, Bull. Inst. Combin. Appl. 19, 17–22 (1997).
↑ Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
↑ Hanson, D. A quick proof that K_10\not= P+P+P, Discrete Math. 101, 107–108 (1992).
↑ ^6.0 ^6.1 Huang, C. and Schönheim, J. Decomposition of K_n into dragons, Canad. Math. Bull. 23, 275–279 (1980).

[_note-adbiho] 1.0 ^1.1 Adams, P., Billington, E. J., and Hoffman, D. G. On the spectrum for K_m+2\sbs K_m designs, J. Combin. Des. 5, 49–60 (1997).

[_note-adbr1] 2.0 ^2.1 Adams, P. and Bryant, D. E. The spectrum problem for the Petersen graph, J. Graph Theory, 22, 175–180 (1996).

[_note-adbr3] 3.0 ^3.1 Adams, P. and Bryant, D. E. The spectrum problem for the Heawood graph, Bull. Inst. Combin. Appl. 19, 17–22 (1997).

[_note-adbrbu] Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).

[_note-ha] Hanson, D. A quick proof that K_10\not= P+P+P, Discrete Math. 101, 107–108 (1992).

[_note-husc] 6.0 ^6.1 Huang, C. and Schönheim, J. Decomposition of K_n into dragons, Canad. Math. Bull. 23, 275–279 (1980).

[1]

[2]

[3]

[4]

[5]

[6]