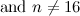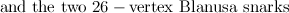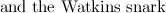Snarks

Results have been obtained for a number snarks. The spectrum problem is completely solved for the Petersen graph, the Tietze graph, the two 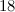$18$ -vertex Blanusa snarks, the six snarks on 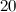$20$ vertices, the twenty snarks on 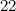$22$ -vertices, and Goldberg's snark 3. 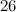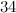Partial results have also been obtained on the two Celmin's-Swart snarks, the two $26$ -vertex Blanusa snarks, the flower snark $J7$ , the double star snark, the two $34$ -vertex Blanusa snarks, Zamfirescu's graph, Goldberg's snark 5, the Szekeres snark, and the Watkins snark.

Spectrum Results

Table 1 summarises the known results on the spectrum problem for various snarks. The reference for each of these results is _^[2], except that the spectrum problem for the Petersen graph was solved in _^[1].

Designs covered by Wilson’s Theorem _^[3] are ignored in the listed possible exceptions in Table 1.

Table 1

*Table 1: The spectrum for some snarks.*
Graph	Spectrum	Possible exceptions
${\rm Petersen\ graph}$	$n \equiv 1 {\rm \ or \ } 10 \,({\rm mod \ }15)$	$\emptyset$
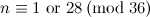
${\rm Tietze\ graph}$	$n \equiv 1 {\rm \ or \ } 28 \,({\rm mod \ }36)$	$\emptyset$
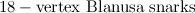
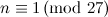
${\rm 18-vertex\ Blanusa\ snarks}$	$n \equiv 1 \,({\rm mod \ }27)$	$\emptyset$
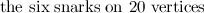
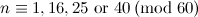
${\rm the\ six\ snarks\ on\ 20\ vertices}$	$n \equiv 1,16,25 {\rm \ or \ } 40 \,({\rm mod \ }60)$ ${\rm and \ } n\neq 16$	$\emptyset$
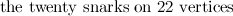
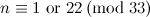
${\rm the\ twenty\ snarks\ on\ 22\ vertices}$	$n \equiv 1 {\rm \ or \ } 22 \,({\rm mod \ }33)$	$\emptyset$
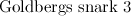
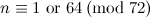
${\rm Goldbergs\ snark\ 3}$	$n \equiv 1 {\rm \ or \ } 64 \,({\rm mod \ }72)$	$\emptyset$
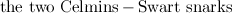
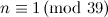
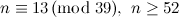
${\rm the\ two\ Celmins-Swart\ snarks}$ ${\rm and\ the\ two\ 26-vertex\ Blanusa\ snarks}$	$n \equiv 1 \,({\rm mod \ }39)$	$n\equiv 13 \,({\rm mod \ }39),\ n\geq 52$
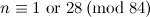
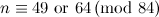
${\rm The\ flower\ snark\ } J_7$	$n \equiv 1 {\rm \ or \ } 28 \,({\rm mod \ }84)$	$n \equiv 49 {\rm \ or \ } 64 \,({\rm mod \ }84)$
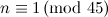
${\rm The\ double\ star\ snark}$	$n \equiv 1 \,({\rm mod \ }45)$	$n \equiv 10 \,({\rm mod \ }45),\ n\geq 55$
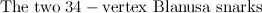
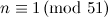
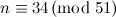
${\rm The\ two\ 34-vertex\ Blanusa\ snarks}$	$n \equiv 1 \,({\rm mod \ }51)$	$n \equiv 34 \,({\rm mod \ }51)$
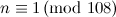
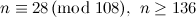
${\rm Zamfirescu's\ graph}$	$n \equiv 1 \,({\rm mod \ }108)$	$n \equiv 28 \,({\rm mod \ }108),\ n\geq 136$
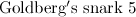
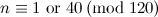
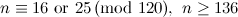
${\rm Goldberg's\ snark\ 5}$	$n \equiv 1 {\rm \ or \ } 40 \,({\rm mod \ }120)$	$n \equiv 16 {\rm \ or \ } 25 \,({\rm mod \ }120),\ n\geq 136$
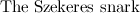
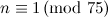
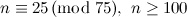
${\rm The\ Szekeres\ snark}$ ${\rm and\ the\ Watkins\ snark}$	$n \equiv 1 \,({\rm mod \ }75)$	$n \equiv 25 \,({\rm mod \ }75),\ n\geq 100$

References

↑ ^1.0 ^1.1 Adams, P. and Bryant, D. E. The spectrum problem for the Petersen graph, J. Graph Theory, 22, 175–180 (1996).
↑ ^2.0 ^2.1 Forbes, A. D. Snark Designs, Preprint,
↑ ^3.0 ^3.1 Wilson, R. M. Decompositions of complete graphs into subgraphs isomorphic to a given graph, Proceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, No. XV, Utilitas Math., Winnipeg, Man. 647–659 (1976).

[_note-adbr1] 1.0 ^1.1 Adams, P. and Bryant, D. E. The spectrum problem for the Petersen graph, J. Graph Theory, 22, 175–180 (1996).

[_note-fo] 2.0 ^2.1 Forbes, A. D. Snark Designs, Preprint,

[_note-wi] 3.0 ^3.1 Wilson, R. M. Decompositions of complete graphs into subgraphs isomorphic to a given graph, Proceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, No. XV, Utilitas Math., Winnipeg, Man. 647–659 (1976).

[1]

[2]

[3]