Theta graphs
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7], [8].
Theta graphs
The theta graph 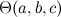 is the graph consisting of three internally disjoint paths with common endpoints and lengths
is the graph consisting of three internally disjoint paths with common endpoints and lengths 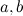 and
and  with
with 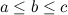 .
.
Spectrum Results
Table 1
summarises the known results on the spectrum problem for theta graphs
with up to nine edges. An explanation of the sources of these results is
given in [1].
Table 1
| Spectrum for theta graphs with 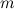 edges edges
| Exceptions |

| 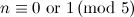
| 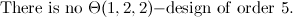
|
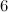
| 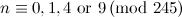
| 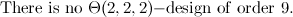
|

| 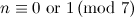
| 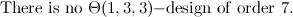
|
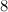
| 
| 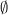
|
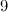
| 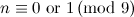
| 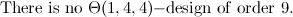
|
Theorem 1 [4]
There exists a 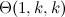 -design of order
-design of order 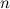 in each of the following cases.
in each of the following cases.
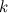 is odd and
is odd and 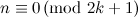 except when
except when 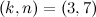 .
.
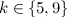 and
and 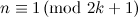 .
.
 and
and 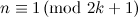 .
.
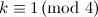 ,
, 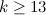 and
and 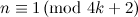 .
.
References
- ↑ 1.0 1.1 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Bermond, J. -C., Huang, C., Rosa, A., and Sotteau, D. Decomposition of complete graphs into isomorphic subgraphs with five vertices, Ars Combin. 10, 211–254 (1980).
- ↑ Bermond, J. -C. and Schönheim, J. $G-decomposition of K_n, where G has four vertices or less, Discrete Math. 19, 113–120 (1977).
- ↑ 4.0 4.1 Blinco, A. On diagonal cycle systems, Australas. J. Combin. 24, 221–230 (2001).
- ↑ Blinco, A. Decompositions of complete graphs into theta graphs with fewer than ten edges, Util. Math. 64, 197–212 (2003).
- ↑ 6.0 6.1 Delorme, C., Maheo, M., Thuillier, H., Koh, K. M., and Teo, H. K. Cycles with a chord are graceful, J. Graph Theory, 4, 409–415 (1980).
- ↑ 7.0 7.1 Koh, K. M. and Yap, K. Y. Graceful numberings of cycles with a P_3-chord, Bull. Inst. Math. Acad. Sinica, 13, 41–48 (1985).
- ↑ 8.0 8.1 Punnim, N. and Pabhapote, N. On graceful graphs: cycles with a P_k-chord, k\geq 4, Ars Combin. 23, 225–228 (1987).
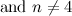
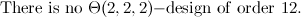
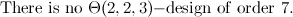
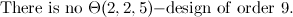
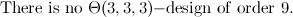
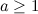 , let
, let 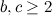 and let
and let 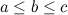 . There exists a
. There exists a 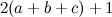 .
.