Complete bipartite graphs
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7].
Contents[hide] |
Complete bipartite graphs
The complete bipartite graph with one part of size  and one part of size
and one part of size 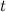 is denoted by
is denoted by 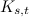 .
.
Spectrum Results
The spectrum problem for complete bipartite graphs has been completely
settled, or almost completely settled, in several small cases, see Table 1. An explanation of the sources of some of these results is given in [1], with additional results obtained by Emre Kolotoglu [6]. Further existence results are given by Theorem 1, while Theorem 2 provides some non-existence results.
Table 1
| Graph | Spectrum | Possible Exceptions |

| 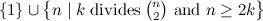
| 
|
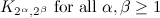
| 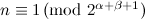
| 
|
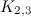
| 
| 
|
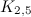
| 
| 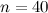
|
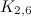
| 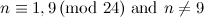
| 
|
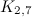
| 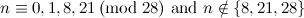
| 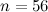
|
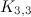
| 
| 
|
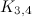
| 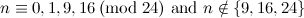
| 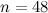
|
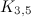
| 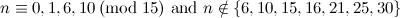
| 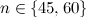
|
Theorem 1 [7]
There exists a 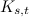 -design of order
-design of order 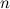 for all
for all 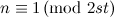 .
.
Some non-existence results for 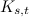 -designs have also been proven and are given in Theorem 2.
-designs have also been proven and are given in Theorem 2.
Notes
- In the case
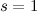 we have stars.
we have stars.
References
- ↑ 1.0 1.1 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Bermond, J. -C., Huang, C., Rosa, A., and Sotteau, D. Decomposition of complete graphs into isomorphic subgraphs with five vertices, Ars Combin. 10, 211–254 (1980).
- ↑ 3.0 3.1 de Caen, D. and Hoffman, D. G. Impossibility of decomposing the complete graph on n points into n-1 isomorphic complete bipartite graphs, SIAM J. Discrete Math. 2, 48–50 (1989).
- ↑ 4.0 4.1 Graham, R. L. and Pollak, H. O. On embedding graphs in squashed cubes, Graph theory and applications (Proc. Conf., Western Michigan Univ., Kalamazoo, Mich., 1972; dedicated to the memory of J. W. T. Youngs), Springer, Berlin, 99–110. lecture notes in math., vol. 303 (1972).
- ↑ Guy, R. K. and Beineke, L. W. The coarseness of the complete graph, Canad. J. Math. 20, 888–894 (1968).
- ↑ 6.0 6.1 Kolotoglu, E. Decomposition of Complete Graphs into Isomorphic Complete Bipartite Graphs, J. Combin. Des. 21, 524 (2013).
- ↑ 7.0 7.1 Rosa, A. On certain valuations of the vertices of a graph, Theory of Graphs (Internat. Sympos., Rome, 1966), Gordon and Breach, New York, 349–355 (1967).
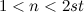 . Moreover, for
. Moreover, for 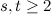 there does not exist a
there does not exist a 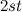 .
.