Stars
From G-designs
Contents[hide] |
Stars
The star on 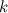 vertices, denoted by
vertices, denoted by 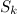 , consists of a vertex
, consists of a vertex  of degree
of degree  , its
, its  neighbours, and the
neighbours, and the  edges joining
edges joining  to its neighbours. Note that stars are trees. Also note that a star
to its neighbours. Note that stars are trees. Also note that a star 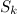 is the complete bipartite graph
is the complete bipartite graph 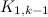 .
.
Spectrum Results
The spectrum problem for stars was completely settled by Yamamoto et al in [2] and independently by Tarsi in [1].
Notes
- Sometimes
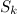 is used to denote a star with
is used to denote a star with 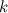 edges, rather than
edges, rather than 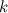 vertices, for example in [3].
vertices, for example in [3].
References
- ↑ 1.0 1.1 Tarsi, M. Decomposition of complete multigraphs into stars, Discrete Math. 26, 273–278 (1979).
- ↑ 2.0 2.1 2.2 Yamamoto, S., Ikeda, H., Shige-eda, S., Ushio, K., and Hamada, N. On claw-decomposition of complete graphs and complete bigraphs, Hiroshima Math. J. 5, 33–42 (1975).
- ↑ Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
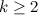 . There exists an
. There exists an 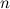 if and only if
if and only if
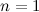 or
or 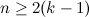 ; and
; and
 .
.