Trees
From G-designs
Cited References: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13].
Contents[hide] |
Trees
The graphs considered in this section are trees (connected
graphs with no cycles). There are two infinite families of trees for
which the spectrum problem is completely solved, namely paths and stars, for details see this page.
Spectrum Results
For 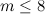 , the following table summarises the known results on the spectrum problem for trees with
, the following table summarises the known results on the spectrum problem for trees with 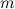 edges. The graphs
edges. The graphs 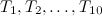 referenced in the table are shown in Figure 1. An explanation of the sources of these results is given in [1].
referenced in the table are shown in Figure 1. An explanation of the sources of these results is given in [1].
Table 1
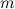
| Spectrum for trees with 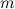 edges edges
| Exceptions (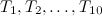 as in Figure 1) as in Figure 1)
|
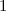
| 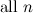
| 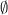
|
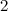
| 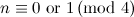
| 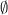
|

| 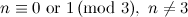
| 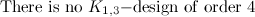
|
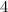
| 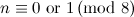
| 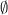
|

| 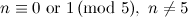
| 
|
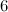
| 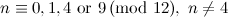
| 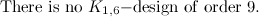
|

| 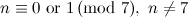
| 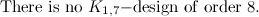
|
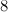
| 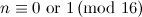
| 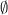
|
The next five theorems provide spectrum results for other families of trees.
More results on labelings of trees, not encompassed by Theorem 1 and Theorem 2, can be found in Gallian's survey 'A dynamic survey of graph labeling' [6].
Theorem 3 [10]
Let 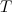 be a caterpillar or lobster with
be a caterpillar or lobster with 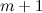 vertices. If
vertices. If  , there exists a
, there exists a 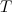 -design of order
-design of order  . Moreover, if
. Moreover, if 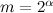 for some integer
for some integer 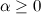 , then
, then 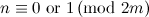 is also necessary for existence.
is also necessary for existence.
Theorem 4 [10]
Let 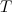 be a tree with
be a tree with 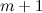 vertices. If
vertices. If 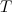 contains a vertex of degree
contains a vertex of degree 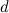 such that
such that 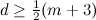 then there does not exist a
then there does not exist a 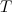 -design of order
-design of order 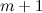 .
.
Theorem 5 [3]
Let 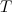 be a tree with
be a tree with 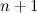 vertices, let
vertices, let  be a vertex in
be a vertex in 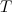 and suppose either of the following holds.
and suppose either of the following holds.
- The graph obtained from
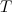 by removing
by removing  (and all the edges incident with
(and all the edges incident with  ) has at least
) has at least 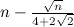 isolated vertices.
isolated vertices.
- For a non-negative integer
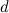 , the diameter of
, the diameter of 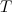 is at most
is at most  , and the graph obtained from
, and the graph obtained from 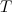 by removing
by removing  (and all the edges incident with
(and all the edges incident with  ) has at least
) has at least 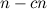 isolated vertices where
isolated vertices where  .
.
Then there exists a 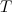 -design of order
-design of order  .
.
Notes
- The base of a graph
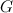 is the graph obtained from
is the graph obtained from 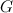 by removing its endvertices.
by removing its endvertices. - A caterpillar is a tree whose base is a path.
- A lobster is a tree whose base is a caterpillar.
- A comet is a graph obtained from a star by replacing each edge with a path of length
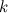 for some fixed
for some fixed 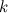 .
. - A tree is symmetric if it can be rooted so that any two vertices in the same level have the same degree.
- Numerous existence results for
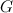 -designs, in particular when
-designs, in particular when 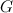 is a tree, have been established under the guise of graph labelings, see [1] for more details.
is a tree, have been established under the guise of graph labelings, see [1] for more details.
References
- ↑ 1.0 1.1 1.2 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ 2.0 2.1 Brankovic, L. and Rosa, A. (private communication).
- ↑ 3.0 3.1 Dobson, E. Packing trees of bounded diameter into the complete graph, Australas. J. Combin. 37, 89–100 (2007).
- ↑ 4.0 4.1 El-Zanati, S. I., Kenig, M. J., and Vanden Eynden, C. Near α-labelings of bipartite graphs, Australas. J. Combin. 21, 275–285 (2000).
- ↑ 5.0 5.1 5.2 El-Zanati, S. I., Vanden Eynden, C., and Punnim, N. On the cyclic decomposition of complete graphs into bipartite graphs, Australas. J. Combin. 24, 209–219 (2001).
- ↑ 6.0 6.1 Gallian, J. A. A dynamic survey of graph labeling, Electron. J. Combin. 5, i (1998).
- ↑ 7.0 7.1 Grannell, M. J., Griggs, T. S., and Holroyd, F. C. Modular gracious labellings of trees, Discrete Math. 231, 199–219 (2001).
- ↑ 8.0 8.1 Hrnčiar, P. and Haviar, A. All trees of diameter five are graceful, Discrete Math. 233, 133–150 (2001).
- ↑ 9.0 9.1 Huang, C., Kotzig, A., and Rosa, A. Further results on tree labellings, Utilitas Math. 21, 31–48 (1982).
- ↑ 10.0 10.1 10.2 Huang, C. and Rosa, A. Decomposition of complete graphs into trees, Ars Combin. 5, 23–63 (1978).
- ↑ 11.0 11.1 Poljak, S. and Sûra, M. An algorithm for graceful labelling of a class of symmetrical trees, Ars Combin. 14, 57–66 (1982).
- ↑ 12.0 12.1 Rosa, A. On certain valuations of the vertices of a graph, Theory of Graphs (Internat. Sympos., Rome, 1966), Gordon and Breach, New York, 349–355 (1967).
- ↑ 13.0 13.1 Zhao, S. L. All trees of diameter four are graceful, Ann. New York Acad. Sci. Graph theory and its applications: East and West (Jinan, 1986), New York Acad. Sci. New York, 700–706 (1989).
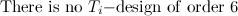
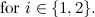
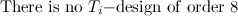


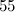 vertices
vertices 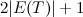 .
.
 vertices
vertices 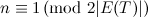 .
.