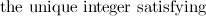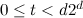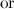Cubes
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7], [8].
Contents[hide] |
Cubes
The 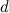 -cube or cube of dimension
-cube or cube of dimension 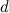 , denoted by
, denoted by 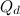 , is the graph with vertex set consisting of all binary strings of length
, is the graph with vertex set consisting of all binary strings of length 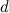 and with two vertices adjacent if and only if they differ in exactly one coordinate.
and with two vertices adjacent if and only if they differ in exactly one coordinate.
Spectrum Results
Table 1 summarises the known results on the spectrum for the 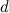 -cube. An explanation of the sources of these results is given in [1].
-cube. An explanation of the sources of these results is given in [1].
Table 1
| Spectrum for the 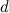 -cube -cube
| Possible exceptions |
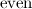
| 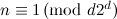
| 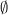
|
| 
| 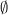
|
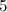
| 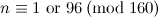
| 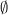
|
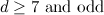
| 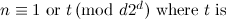
| 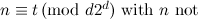
|
Theorem 1 [5]
Let 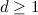 be odd, let
be odd, let 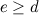 be such that
be such that 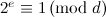 and let
and let  be the order of
be the order of 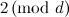 . If
. If 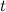 is a non-negative integer and
is a non-negative integer and 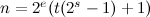 , then there exists a
, then there exists a 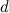 -cube-design of order
-cube-design of order 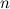 .
.
Theorem 2 [4]
Let 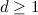 be odd and let
be odd and let 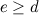 be such that
be such that 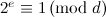 . If
. If 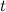 is a non-negative integer and
is a non-negative integer and 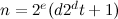 , then there exists a
, then there exists a 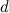 -cube-design of order
-cube-design of order 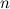 .
.
Notes
- The
 -cube is a single edge and the spectrum is trivially the set of all positive integers.
-cube is a single edge and the spectrum is trivially the set of all positive integers.
- The
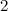 -cube is a
-cube is a  -cycle and the spectrum is well known to be all
-cycle and the spectrum is well known to be all  (see the section on cycles).
(see the section on cycles).
References
- ↑ 1.0 1.1 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Bryant, D. E., El-Zanati, S. I., and Gardner, R. B. Decompositions of K_m,n and K_n into cubes, Australas. J. Combin. 9, 285–290 (1994).
- ↑ Bryant, D., El-Zanati, S. I., Maenhaut, B., and Vanden Eynden, C. Decomposition of complete graphs into 5-cubes, J. Combin. Des. 14, 159–166 (2006).
- ↑ 4.0 4.1 Buratti, M. (private communication).
- ↑ 5.0 5.1 El-Zanati, S. I. and Vanden Eynden, C. Decomposing complete graphs into cubes, Discuss. Math. Graph Theory, 26, 141–147 (2006).
- ↑ Kotzig, A. Decompositions of complete graphs into isomorphic cubes, J. Combin. Theory Ser. B, 31, 292–296 (1981).
- ↑ Maheo, M. Strongly graceful graphs, Discrete Math. 29, 39–46 (1980).
- ↑ Wilson, R. M. Decompositions of complete graphs into subgraphs isomorphic to a given graph, Proceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, No. XV, Utilitas Math., Winnipeg, Man. 647–659 (1976).