Even graphs
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11].
Contents[hide] |
Even graphs
A graph is even if each vertex has even degree.
A 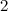 -regular graph is a union of vertex disjoint cycles.
-regular graph is a union of vertex disjoint cycles.
We denote by 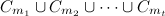 the
the 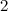 -regular graph consisting of
-regular graph consisting of 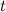 vertex disjoint cycles of lengths
vertex disjoint cycles of lengths  .
.
An even graph which is connected is called a closed trail, and a closed trail with 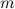 edges is a called a closed
edges is a called a closed 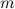 -trail.
-trail.
Spectrum Results
Table 1
summarises the known results on the spectrum problem for even graphs
with up to ten edges. An explanation of the sources of these results is
given in [1].
Table 1
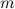
| Spectrum for each even graph with 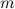 edges edges
| Exceptions ( and and  as in Figure 1) as in Figure 1)
|
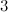
| 
| 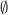
|
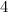
| 
| 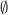
|
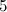
| 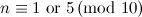
| 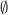
|

| 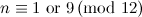
| 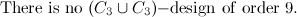
|

| 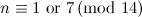
| 
|
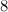
| 
| 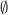
|
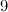
| 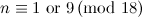
| 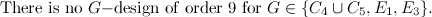
|
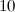
| 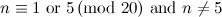
| 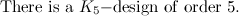
|
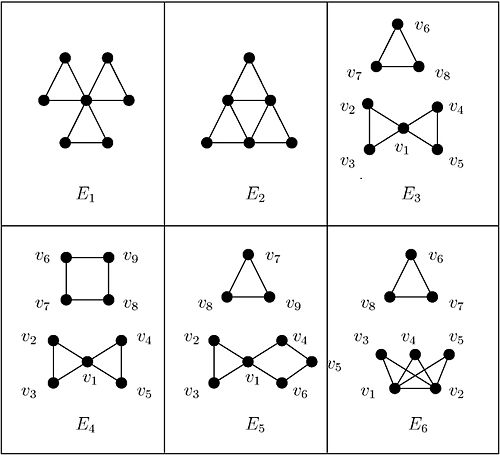
Theorem 1 [7]
Let 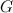 be a
be a 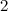 -regular bipartite graph. There exists a
-regular bipartite graph. There exists a 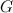 -design of order
-design of order 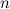 for all
for all 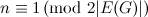 .
.
Theorem 2 [4]
Let 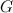 be a
be a 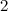 -regular graph with at most three components. There exists a
-regular graph with at most three components. There exists a 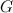 -design of order
-design of order 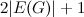 .
.
Theorem 4 [9]
Let 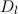 be the union of
be the union of 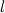 edge-disjoint
edge-disjoint 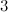 -cycles each sharing a common vertex. If
-cycles each sharing a common vertex. If 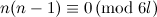 and
and  then there exists a
then there exists a 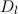 -design of order
-design of order 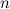 .
.
Notes
- It is well-known (though at present there is no published proof, see [5]) that there is no
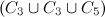 -design of order
-design of order 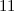 .
.
- Results on the famous Oberwolfach problem provide further
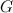 -designs of orders
-designs of orders 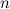 for many instances where
for many instances where 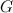 is a
is a 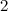 -regular graph with
-regular graph with 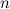 vertices, see the section on unions of graphs.
vertices, see the section on unions of graphs.
- When
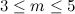 the only closed
the only closed 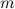 -trails are cycles (see the section on cycles).
-trails are cycles (see the section on cycles).
- When
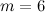 we have only the
we have only the  -cycle and the graph
-cycle and the graph 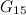 (see Figure 1 in the section on Graphs with five vertices).
(see Figure 1 in the section on Graphs with five vertices).
- A Dutch
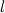 -windmill, denoted
-windmill, denoted 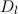 , is the graph containing a vertex,
, is the graph containing a vertex,  say, such that
say, such that 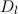 is the union of
is the union of 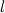 edge-disjoint 3-cycles, all of which contain the vertex
edge-disjoint 3-cycles, all of which contain the vertex  .
. - There are four even graphs with
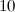 or fewer vertices which are neither
or fewer vertices which are neither 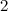 -regular nor closed trails, namely the graphs
-regular nor closed trails, namely the graphs  ,
, 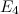 ,
, 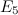 and
and  shown in Figure 1.
shown in Figure 1.
References
- ↑ 1.0 1.1 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Adams, P., Bryant, D., and Gavlas, H. Decompositions of the complete graph into small 2-regular graphs, J. Combin. Math. Combin. Comput. 43, 135–146 (2002).
- ↑ Adams, P., Bryant, D. E., and Khodkar, A. The spectrum problem for closed m-trails, m\leq 10, J. Combin. Math. Combin. Comput. 34, 223–240 (2000).
- ↑ 4.0 4.1 Aguado, A., El-Zanati, S. I., Hake, H., Stob, J., and Yayla, H. On ρ-labeling the union of three cycles, Australas. J. Combin. 37, 155–170 (2007).
- ↑ 5.0 5.1 Alspach, B. The Oberwolfach problem, CRC Press Series on Discrete Mathematics and its Applications, The CRC handbook of combinatorial designs, ed. 1, CRC Press, 394–395 (1996).
- ↑ Bermond, J. -C., Huang, C., Rosa, A., and Sotteau, D. Decomposition of complete graphs into isomorphic subgraphs with five vertices, Ars Combin. 10, 211–254 (1980).
- ↑ 7.0 7.1 Blinco, A. and El-Zanati, S. I. A note on the cyclic decomposition of complete graphs into bipartite graphs, Bull. Inst. Combin. Appl. 40, 77–82 (2004).
- ↑ 8.0 8.1 Dinitz, J. H. and Rodney, P. Disjoint difference families with block size 3, Util. Math. 52, 153–160 (1997).
- ↑ 9.0 9.1 9.2 Horák, P. and Rosa, A. Decomposing Steiner triple systems into small configurations, Ars Combin. 26, 91–105 (1988).
- ↑ Köhler, E. Über das Oberwolfacher Problem, Lehrbücher Monograph. Geb. Exakten Wissensch., Math. Reihe, Beiträge zur geometrischen Algebra (Proc. Sympos., Duisburg, 1976), Birkhäuser, Basel, 189–201 (1977).
- ↑ Mullin, R. C., Poplove, A. L., and Zhu, L. Decomposition of Steiner triple systems into triangles, Proceedings of the first Carbondale combinatorics conference (Carbondale, Ill., 1986), 149–174 (1987).
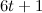
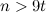 there exists a
there exists a