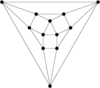
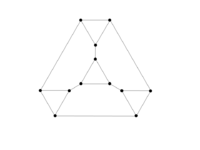
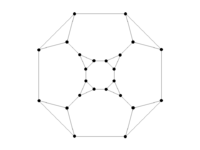
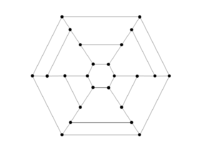
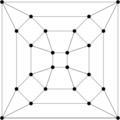
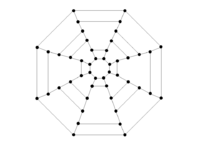
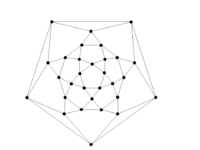
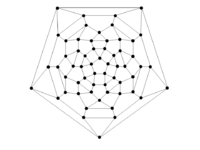
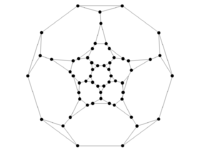
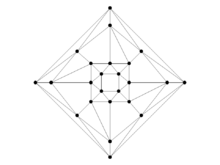
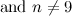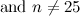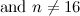Graphs of Geometric Solids
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12].
Contents[hide] |
Graphs of Geometric Solids
Results have been obtained on the 5 Platonic solids, on 12 of the 13 Archimedean solids, and also on the Pseudo-rhombicuboctahedron.
|
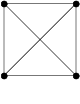
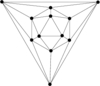
Tetrahedron |
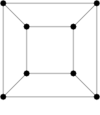
Cube |
Octahedron |
|
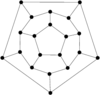
Dodecahedron |
Icosahedron |
Cuboctahedron |
|
Truncated Tetrahedron |
Truncated Cube |
Truncated Octahedron |
|
Rhombicuboctahedron |
Truncated Cuboctahedron |
Icosidodecahedron |
|
Rhombicosidodecahedron |
Truncated Icosahedron |
Truncated Dodecahedron |
|
Truncated Icosidodecahedron |
Snub Cube |
Pseudo-rhombicuboctahedron |
Spectrum Results
Table 1
summarises the known results on the spectrum problem for the 5 Platonic
solids (the tetrahedron, the cube, the octahedron, the dodecahedron and
the icosahedron), the 13 Archimedean solids (the cuboctahedron, the
truncated tetrahedron, the trucated cube, the truncated octahedron, the
rhombicuboctahedron, the truncated cuboctahedron, the icosidodecahedron,
the rhombicosidodecahedron, the truncated icosahedron, the truncated
dodecahedron, the truncated icosidodecahedron, the snub cube and the
snub dodecahedron) and the pseudo-rhombicuboctahedron. An explanation of
the sources of most of these results is given in [3]. New results, coming after [3] was published, and a correction to [3] are discussed below.
The spectrum problem for the octahedron was solved in 1992 by Griggs et al [10], with the exception that the case 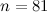 was left unresolved. An octahedron design of order
was left unresolved. An octahedron design of order 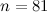 was subsequently constructed by Adams et al in [1]. In [3], the solution of the spectrum problem for the octahedron was incorrectly attributed to Horak and Rosa [11].
was subsequently constructed by Adams et al in [1]. In [3], the solution of the spectrum problem for the octahedron was incorrectly attributed to Horak and Rosa [11].
The spectrum problem for the rhombicuboctahedron was completely solved by Forbes et al [5].
The spectrum problem for the dodecahedron was completed by Adams, Bryant, Forbes and Griggs [4].
The spectrum problems for the truncated tetrahedron, the truncated cube and the trucated octahedron were completely solved by Forbes, Griggs and Holroyd [6].
The spectrum problem for the icosahedron was completed, except that the existence of an icosahedron design of order 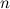 is left unresolved for
is left unresolved for 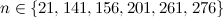 , by Forbes and Griggs [7].
, by Forbes and Griggs [7].
Forbes and Griggs [8] have shown that if 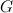 is the graph of the truncated cuboctahedron, the icosidodecahedron, the
rhombicosidodecahedron, the truncated icosahedron, the truncated
dodecahedron, the truncated icosidodecahedron or the snub cube, then
there is a
is the graph of the truncated cuboctahedron, the icosidodecahedron, the
rhombicosidodecahedron, the truncated icosahedron, the truncated
dodecahedron, the truncated icosidodecahedron or the snub cube, then
there is a 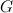 -design of order
-design of order 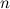 for all
for all 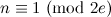 where
where  is the number of edges in
is the number of edges in 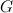 . Also in [8], the spectrum problem is completely solved for the graph of the pseudo-rhombicuboctahedron and it is shown that there exists a
. Also in [8], the spectrum problem is completely solved for the graph of the pseudo-rhombicuboctahedron and it is shown that there exists a 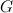 -design of order
-design of order 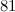 where
where 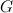 is the graph of the icosidodecahedron, and that there exists a
is the graph of the icosidodecahedron, and that there exists a 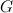 -design of order
-design of order  where
where 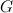 is the graph of the truncated dodecahedron.
is the graph of the truncated dodecahedron.
There are currently no known results on the spectrum problem for the snub dodecahedron.
Designs covered by Wilson’s Theorem [12] are ignored in the listed possible exceptions in Table 1.
| Graph | Spectrum | Possible exceptions |
| 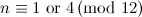
| 
|
| 
| 
|
| 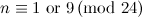
| 
|
| 
| 
|
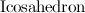
| 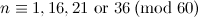
| 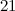 , , 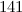 , , 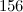 , , 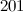 , ,  and and 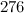
|
| 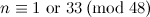
| 
|
| 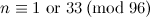
| 
|
| 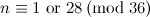
| 
|
| 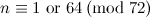
| 
|
| 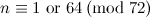
| 
|
| 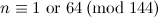
| 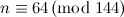
|
| 
|  with with 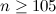
|

| 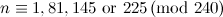
| 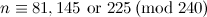
|
| 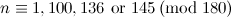
| 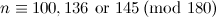
|
| 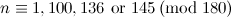
| 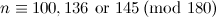 with with 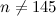
|
| 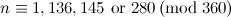
| 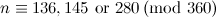
|

| 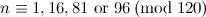
| 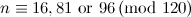 with with 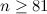
|
| 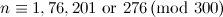
| 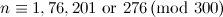
|
| 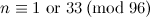
| 
|
Notes
- The tetrahedron, being the complete graph on four vertices, is covered in the section on complete graphs.
- The cube is covered in section on cubes.
References
- ↑ 1.0 1.1 Adams, P., Billington, E. J., and Rodger, C. A. Pasch decompositions of lambda-fold triple systems, J. Combin. Math. Combin. Comput. 15, 53–63 (1994).
- ↑ Adams, P. and Bryant, D. E. Decomposing the complete graph into Platonic graphs, Bull. Inst. Combin. Appl. 17, 19–26 (1996).
- ↑ 3.0 3.1 3.2 3.3 3.4 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ 4.0 4.1 Adams, P., Bryant, D., Forbes, A. D., and Griggs, T. S. The completion of the spectrum problem for the Dodecahedron, Preprint,
- ↑ 5.0 5.1 Forbes, A. D., Griggs, T. S., and Holroyd, F. C. Rhombicuboctahedron designs, J. Combin. Math. Combin. Comput. 75, 161 (2010).
- ↑ 6.0 6.1 Forbes, A. D., Griggs, T. S., and Holroyd, F. C. Truncated tetrahedron, octahedron and cube designs, Submitted,
- ↑ 7.0 7.1 Forbes, A. D. and Griggs, T. S. Icosahedron Designs, Preprint,
- ↑ 8.0 8.1 8.2 Forbes, A. D. and Griggs, T. S. Archimedean Graph Designs, Preprint,
- ↑ Grannell, M. J., Griggs, T. S., and Holroyd, F. C. Cuboctahedron designs, J. Combin. Math. Combin. Comput. 35, 185–191 (2000).
- ↑ 10.0 10.1 Griggs, T. S., de Resmini, M. J., and Rosa, A. Decomposing Steiner triple systems into four-line configurations, 52, 215–226 (1992).
- ↑ 11.0 11.1 Horák, P. and Rosa, A. Decomposing Steiner triple systems into small configurations, Ars Combin. 26, 91–105 (1988).
- ↑ 12.0 12.1 Wilson, R. M. Decompositions of complete graphs into subgraphs isomorphic to a given graph, Proceedings of the Fifth British Combinatorial Conference (Univ. Aberdeen, Aberdeen, 1975), Congressus Numerantium, No. XV, Utilitas Math., Winnipeg, Man. 647–659 (1976).