Graphs with four or fewer vertices
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6].
Contents[hide] |
Graphs with four or fewer vertices
There are ten non-isomorphic graphs with four or fewer vertices,
excluding those with isolated vertices, and these are shown in the Figure 1.
Spectrum Results
The spectrum problem is completely settled for graphs all with up to four vertices, excluding those with isolated vertices, and Table 1 summarises these results. An explanation of the sources of these results is given in [1].
Table 1
| Graph | Spectrum |
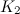
| 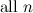
|
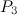
| 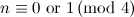
|
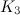
| 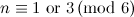
|
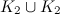
| 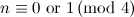
|
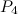
| 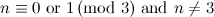
|

| 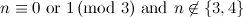
|
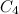
| 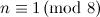
|
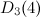
| 
|
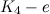
| 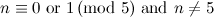
|

| 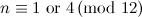
|
Notes
- The complete graphs
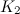 ,
, 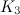 and
and 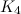 are discussed in the section on complete graphs.
are discussed in the section on complete graphs.
- The spectrum problems for the path
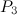 and the graph
and the graph 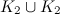 are easy exercises, and their solutions are covered by Theorem 1 in the section on Paths and Theorem 1 in the section on Matchings.
are easy exercises, and their solutions are covered by Theorem 1 in the section on Paths and Theorem 1 in the section on Matchings.
- A solution for
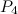 is also given by Theorem 1 in the section on Paths.
is also given by Theorem 1 in the section on Paths.
- Note that
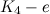 is a
is a  -graph.
-graph.
- Also note that
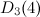 is a dragon.
is a dragon.
References
- ↑ 1.0 1.1 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Bermond, J. -C. Cycles dans les graphes et G-configurations, PhD Thesis (1975).
- ↑ Bermond, J. -C. and Schönheim, J. $G-decomposition of K_n, where G has four vertices or less, Discrete Math. 19, 113–120 (1977).
- ↑ Cain, P. Decomposition of complete graphs into stars, Bull. Austral. Math. Soc. 10, 23–30 (1974).
- ↑ Kotzig, A. Decomposition of a complete graph into 4k-gons, Mat.-Fyz. u Casopis Sloven. Akad. Vied, 15, 229–233 (1965).
- ↑ Tarsi, M. Decomposition of a complete multigraph into simple paths: nonbalanced handcuffed designs, J. Combin. Theory Ser. A, 34, 60–70 (1983).
 vertices
vertices
