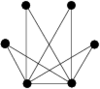
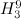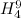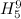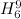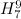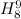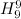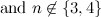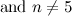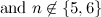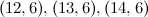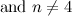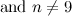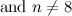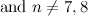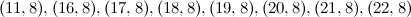Graphs with six vertices
From G-designs
Relevant articles: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15].
Contents[hide] |
Graphs with six vertices
This page summarises the known results on the spectrum problem for
graphs with six vertices. The majority of these results are concerned
with graphs on six vertices with at most nine edges. However, there are a
few other results on graphs on six vertices with more than nine edges.
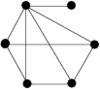
The first results considered are for all graphs on six vertices with at most eight edges, excluding those with isolated vertices (see Table 1). Next the known results for graphs on six vertices with nine edges, excluding those with isolated vertices, are discussed (see Table 2). Finally the known results for graphs with six vertices and more than nine edges, excluding those with isolated vertices, are described.
There are 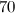 non-isomorphic graphs on six vertices with at most eight edges,
excluding those with isolated vertices, and these are shown in the Figure 1.
non-isomorphic graphs on six vertices with at most eight edges,
excluding those with isolated vertices, and these are shown in the Figure 1.
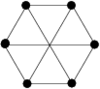
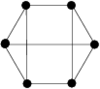
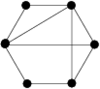
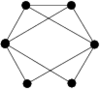
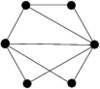
There are twenty one non-isomorphic graphs with six vertices and nine edges, excluding those with isolated vertices. The spectrum problem has been completely solved for ten of these which are shown in Figure 2.
Spectrum Results
Table 1 summarises the known results on the spectrum problem for graphs with 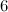 vertices and up to
vertices and up to 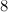 edges. An explanation of the sources of most of these results is given in [2], and the remainder are new results as discussed below.
edges. An explanation of the sources of most of these results is given in [2], and the remainder are new results as discussed below.
The results from [12] left possible exceptions for the graph 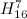 (which are listed as such in [2]). These exceptions have since been dealt with in [14] and they are included in Table 1.
(which are listed as such in [2]). These exceptions have since been dealt with in [14] and they are included in Table 1.
Table 1
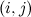
| Spectrum for 
| Possible
exceptions |
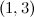
| 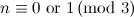
| 
|
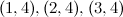
| 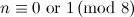
| 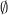
|
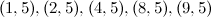
| 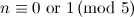
| 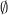
|
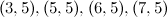
| 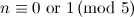
| 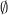
|
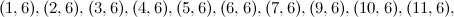
| 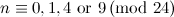
| 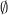
|
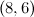
| 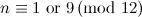
| 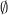
|
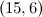
| 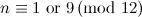
| 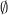
|
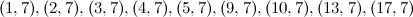
| 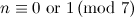
| 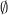
|
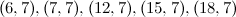
| 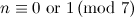
| 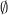
|
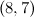
| 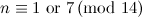
| 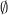
|
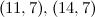
| 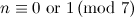
| 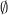
|
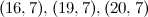
| 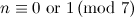
| 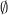
|
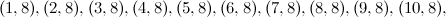
| 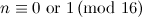
| 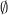
|
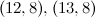
| 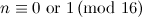
| 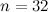
|
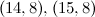
| 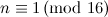
| 
|
There are twenty one non-isomorphic graphs with six vertices and nine edges, excluding those with isolated vertices. The spectrum problem has been solved for the ten of these shown in Figure 2, and the results are summarised in Table 2.
In [10], the spectrum problem is completely solved for 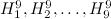 and the spectrum problem for
and the spectrum problem for 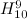 is solved in [1]. The spectrum problems for
is solved in [1]. The spectrum problems for 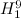 and
and 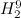 were solved prior to [10]. The spectrum problem for the graph
were solved prior to [10]. The spectrum problem for the graph 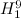 was first solved by Mullin et al [11] (see the page on even graphs), and the spectrum problem for
was first solved by Mullin et al [11] (see the page on even graphs), and the spectrum problem for 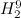 (the complete bipartite graph
(the complete bipartite graph 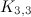 ) was first solved by Guy and Beineke [5] (see the page on complete bipartite graphs).
) was first solved by Guy and Beineke [5] (see the page on complete bipartite graphs).
Table 2
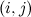
| Spectrum for 
|
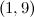
| 
|

| 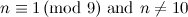
|

| 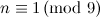
|
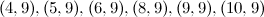
| 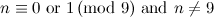
|
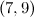
| 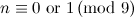
|
The known results for graphs with six vertices and more than nine edges, excluding those with isolated vertices, are described below.
The spectrum for the unique closed 10-trail on six vertices is dealt with in the section on even graphs.
The known results on the spectrum problem for 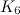 are covered in the section on complete graphs.
are covered in the section on complete graphs.
In [7] it is shown by computer search that there is no 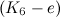 -design of order
-design of order 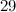 (
(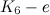 is the graph obtained by removing an edge from
is the graph obtained by removing an edge from 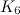 ). This is the only known example of a non-complete graph,
). This is the only known example of a non-complete graph, 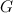 say, such that there is no
say, such that there is no 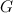 -design of order
-design of order 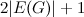 .
.
Notes
- The spectrum problem for
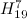 and
and 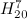 is settled in [4]. However, as [4] is not easily accessible the construction is included in [2].
is settled in [4]. However, as [4] is not easily accessible the construction is included in [2].
- Some of the graphs in this section belong to special families and have thus been covered in other sections of this site. For example, some are trees, even graphs, matchings or theta graphs.
- In [10] the authors incorrectly state that there are twenty non-isomorphic graphs with six vertices and nine edges, excluding those with isolated vertices. There are in fact twenty one (see [6] and [13]).
References
- ↑ 1.0 1.1 Adams, P., Billington, E. J., and Hoffman, D. G. On the spectrum for K_m+2\sbs K_m designs, J. Combin. Des. 5, 49–60 (1997).
- ↑ 2.0 2.1 2.2 2.3 Adams, P., Bryant, D., and Buchanan, M. A survey on the existence of G-designs, J. Combin. Des. 16, 373–410 (2008).
- ↑ Adams, P., Bryant, D. E., and Khodkar, A. The spectrum problem for closed m-trails, m\leq 10, J. Combin. Math. Combin. Comput. 34, 223–240 (2000).
- ↑ 4.0 4.1 4.2 Cui, Y. G. Decompositions and packings of λK_v into K_2,s with a pendant edge, PhD Thesis (2002).
- ↑ 5.0 5.1 Guy, R. K. and Beineke, L. W. The coarseness of the complete graph, Canad. J. Math. 20, 888–894 (1968).
- ↑ 6.0 6.1 Harary, F. Graph theory, Addison-Wesley Publishing Co., Reading, Mass.-Menlo Park, Calif.-London, (1969).
- ↑ 7.0 7.1 Hartke, S. G., Östergård, P. R. J., Bryant, D., and El-Zanati, S. I. The nonexistence of a (K_6-e)-decomposition of the complete graph K_29, J. Combin. Des. 18, 94–104 (2010).
- ↑ Huang, C. and Rosa, A. Decomposition of complete graphs into trees, Ars Combin. 5, 23–63 (1978).
- ↑ Kang, Q., Yuan, L., and Liu, S. Graph designs for all graphs with six vertices and eight edges, Acta Math. Appl. Sin. Engl. Ser. 21, 469–484 (2005).
- ↑ 10.0 10.1 10.2 10.3 Kang, Q., Zhao, H., and Ma, C. Graph designs for nine graphs with six vertices and nine edges, Ars Combin. 88, 379–395 (2008).
- ↑ 11.0 11.1 Mullin, R. C., Poplove, A. L., and Zhu, L. Decomposition of Steiner triple systems into triangles, Proceedings of the first Carbondale combinatorics conference (Carbondale, Ill., 1986), 149–174 (1987).
- ↑ 12.0 12.1 Tian, Z., Du, Y., and Kang, Q. Decomposing complete graphs into isomorphic subgraphs with six vertices and seven edges, Ars Combin. 81, 257–279 (2006).
- ↑ 13.0 13.1 Read, R. C. and Wilson, R. J. An atlas of graphs, Oxford Science Publications, New York:The Clarendon Press Oxford University Press, (1998).
- ↑ 14.0 14.1 Wang, L. The spectrum for a class of graph designs, Preprint, (2009).
- ↑ Yin, J. X. and Gong, B. S. Existence of G-designs with \vert V(G)\vert =6, Lecture Notes in Pure and Appl. Math. Combinatorial designs and applications (Huangshan, 1988), Dekker, New York, 201–218 (1990).
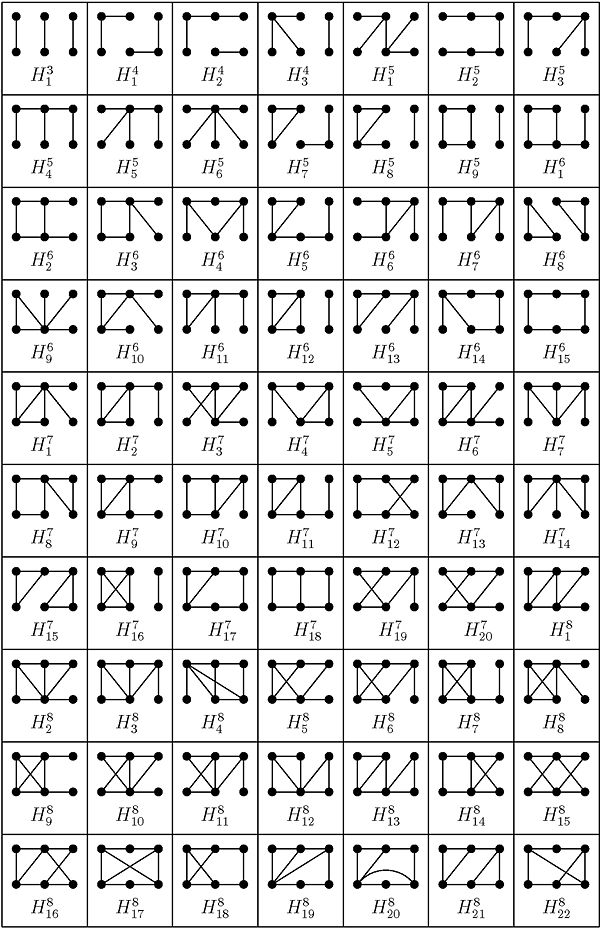
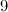 edges.
edges.